How It Works
Traditional four-in-a-row games are played on a rectangular grid. That is to say, if the game board were a piece of graphing paper, you’d have an x-axis (horizontal) and a y-axis (vertical).
When placing pieces, you and your opponent imagine that the board is standing upright, which means that a piece placed in any given column should always fall to the lowest available row. (And, of course, if you’ve bought a popular version of this game available in many toy stores, there is no imagination required; the board really does stand upright and the pieces really do fall!)
Polar Connection, on the other hand, is a four-in-a-row game played on a grid inspired by the polar coordinate system. While many of the basic gameplay mechanics are the same, the shape of the board makes the experience quite different.
If you’re not familiar with polar coordinates or can’t remember the details from that math class you took oh-so-many years ago, here’s a quick tutorial on how that works and how it changes the rules of the game.
What are polar coordinates?
In the polar coordinate system, there is no left or right, up or down. Instead, you represent locations in terms of circles; in the very center of the grid, you have the origin, and then you have what is essentially an infinite series of concentric circles expanding outward from the center.

To find a particular point (or location) on the grid, you need to know two things:
- The radius, which tells you which how far away from the origin the point is—or, essentially, which circle the point is part of. (Remember that a circle is defined as a shape for which all points along its “edge” are the same distance, or radius, from the center.)
- The angle, which tells you where along the edge of that circle you can find the desired point. (When measuring the angle, you typically start from the line pointing to the right from the origin and proceed counterclockwise around the circle.)
In the rectangular coordinate system, also known as the Cartesian coordinate system, you define the location of a point as ( x , y ) to represent that point’s distance from the x-axis and y-axis, respectively. In the polar coordinate system, you define the location of a point as ( r , 𝜃 ), which corresponds to the radius and angle as described above.
How do you play four-in-a-row like this?
The good news is that you don’t actually need to understand how to plot points on a graph to play the game. There are a few things we do have to consider, though.
The first thing we need to think about is how gravity should work. Since there is no up or down on this grid, the most logical center of gravity is, well, the center of the grid. Anything placed on the grid should “fall” towards the center (i.e. the origin).
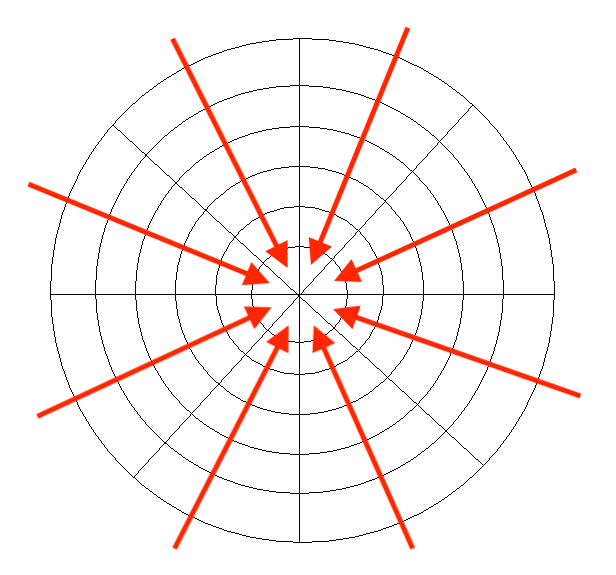
After that, the rest is somewhat intuitive. For example, instead of trying to get four pieces in a row horizontally, you would aim to create rings (pieces that connect along a circle).
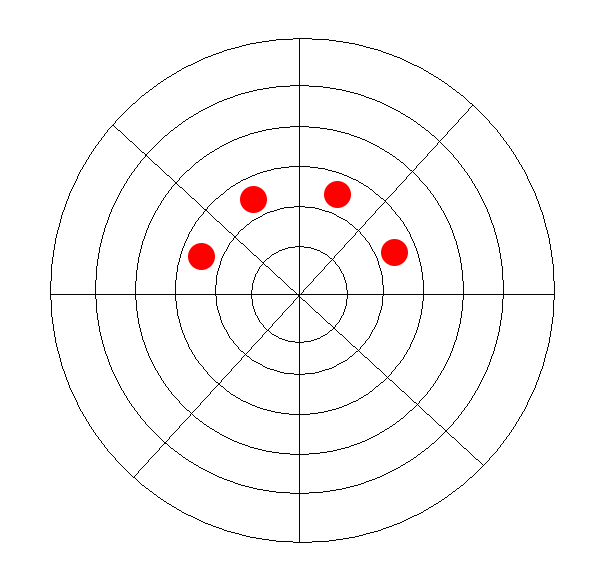
Meanwhile, you could still try to create columns of pieces; however, instead of stacking them vertically, the columns would extend outward from the center. For simplicity’s sake, I’m just going to call these lines.
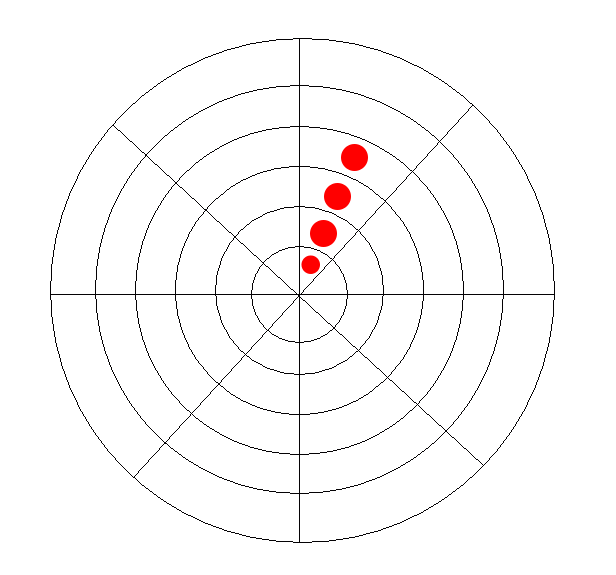
Diagonals would still exist as well, but in this game they would more closely resemble spirals.
So what’s the point?
As you can see from above, the basic mechanics are the same. There are essentially three ways to get four-in-a-row: rings are like rows, lines are like columns, and spirals are like diagonals.
What makes the actual gameplay different from traditional four-in-a-row is that there are fewer edges!
On a rectangular game board, there are four edges. A set of consecutive pieces must stop at either the bottom, the left, the right, or the top. However, on this polar game board, the only true edge is the outermost circle.
This has a few interesting implications. First, because circles are essentially infinite, rings and spirals can start and end anywhere. There are no boundaries to get in your way!
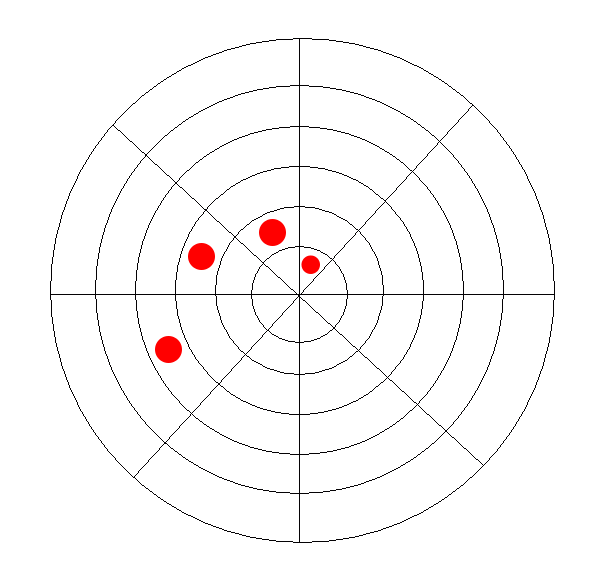
The second implication is a little stranger. From a geometrical standpoint, there’s really nothing to stop a line from crossing through the origin. So this enables win conditions like the following that could not exist in a typical four-in-a-row game:
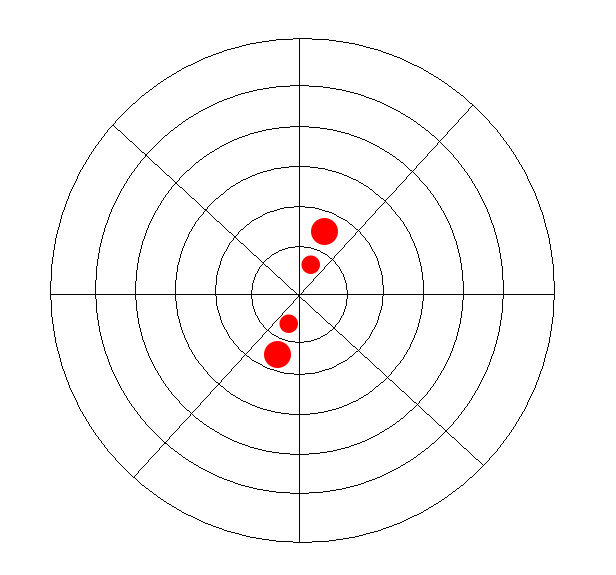
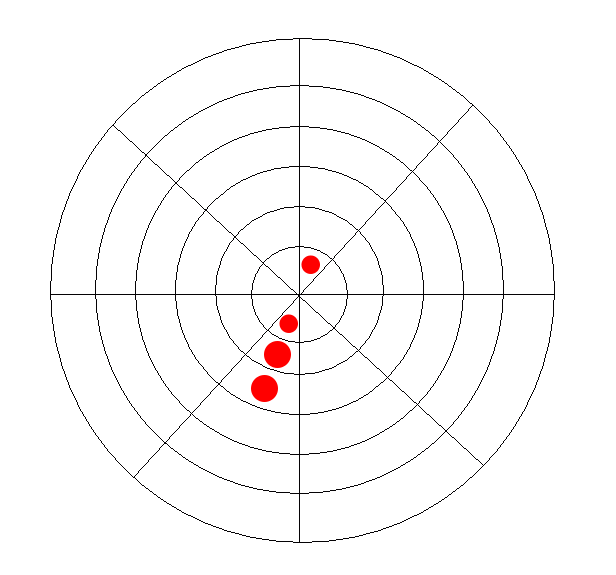
One might be tempted to suggest that spirals could cross through the origin as well. When my friends and I first explored this game back in our high school math class, we found this really hard to conceptualize. So, to avoid that particular geometric nightmare, we decided that this should not be allowed.
Putting It All Together
That leaves us with the following set of rules:
- Players take turns adding their pieces to the board. Only one piece may be added per turn.
- Pieces must “fall” towards the center of the board. This means that a piece can only be played in a particular location if that spot is empty and the adjacent spot that is closer to the center of the board is NOT empty. (This rule does not apply to the innermost ring. As long as a location in that ring is empty, it is always a valid spot.)
- A player wins by placing four of their own pieces side by side. These pieces may form a ring, line, or spiral. Lines (and only lines) may cross through the center of the board.
And that’s it! If you decide to play again, the winner of the previous game starts the next one.
Ready to Play?
Visit the download page if you haven’t already done so to get the latest copy of Polar Connection! You can challenge a friend or try your hand against the computer opponent.
And if you’re still feeling a little confused, just try clicking one of the “Drop” buttons on the game board. Your piece will automatically be placed in the appropriate location. After a few rounds, the mechanics should become clear.
You can also play your turn by clicking directly on the spot you want to fill. If your desired move is valid, the spot will light up faintly before you click. (If you’re having trouble figuring out where to click, go to the View menu and select Show Empty Spots.)